이산형 확률분포
1. 이산균일분포
- n 개의 결과값이 균일한 확률로 발생하는 확률분포
2. 이항분포
- 성공확률이 일정한 n회의 시행에서 나오는 성공 횟수의 확률분포


기댓값

분산

실습코드
import scipy.stats as spt
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Binomial distribution 이항분포
fig, ax = plt.subplots(1, 1)
n=70; p=0.4;
m,var,skw,kur=spt.binom.stats(n,p,moments='mvsk')
#n 횟수, #moment
print(m,var,skw,kur)
x = np.arange(spt.binom.ppf(0.01, n, p),spt.binom.ppf(0.99, n, p))
# cdf: 누적확률분포(0부터1)
# ppf: cdf의 역, 누적확률분포가 1%인 n 과 p의 값
ax.plot(x, spt.binom.pmf(x, n, p), 'ro', ms=8, label='binomial pmf')
ax.vlines(x, 0, spt.binom.pmf(x, n, p), colors='g', lw=5, alpha=0.3)
#그래프에서는 보통 alpha 투명도
plt.show()
rv=spt.binom.rvs(n,p,size=10)
print('random variable\t',rv)

베르누이분포: 성광 확률이 일정한 1회의 시행에서 나오는 성공 횟수의 확률분포
3. 포아송분포
- 일정한 단위에서 발생한 희소한 사건수의 확률분포
- 도착확률

실습코드
# Poisson distribution
fig, ax = plt.subplots(1, 1)
mu = 0.6
m,var,skw,kur = spt.poisson.stats(mu,moments='mvsk')
print(m,var,skw,kur)
#분산과 평균이 같다.
x = np.arange(spt.poisson.ppf(0.01, mu),spt.poisson.ppf(0.99, mu))
ax.plot(x, spt.poisson.pmf(x, mu), 'ro', ms=8, label='poisson pmf')
ax.vlines(x, 0, spt.poisson.pmf(x, mu), colors='g', lw=5, alpha=0.3)
plt.show()
rv=spt.poisson.rvs(mu,size=10)
print('random variable\t',rv)
연속형 확률분포
1. 균일분포
- 유한한 실수 구간 [a,b]에서 동일한 확률로 관측된는 확률변수의 분포


기댓값
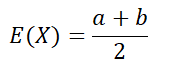
분산

2. 지수분포
- 확률밀도함수가 지수적으로 감소하는 확률분포
- 고장확률, 인구증가, 주가 등
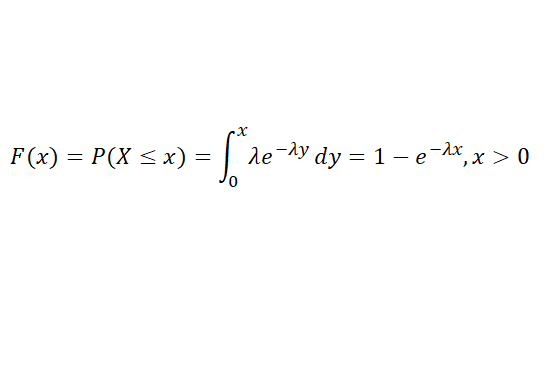
기댓값

분산

실습코드
#exponential distribution
fig, ax = plt.subplots(1, 1)
m, var, skw, kur = spt.expon.stats(moments='mvsk')
print(m,var,skw,kur)
x = np.linspace(spt.expon.ppf(0.01),spt.expon.ppf(0.99), 100)
ax.plot(x, spt.expon.pdf(x),'r-', lw=5, alpha=0.6, label='exponential pdf')
rv = spt.expon.rvs(size=300)
ax.hist(rv, density=True, histtype='stepfilled', alpha=0.2)
plt.show()

지수분포의 비기억(memoryless) 특성

정규 분포와 관련 분포
1. 정규분포
- 기댓값을 중심으로 대칭이며, 중심위치는 기댓값, 산포는 표준편차에 의해 결정된는 엎어 놓은 종 모양의 분포


실습코드
# Normal distribution
fig, ax = plt.subplots(1, 1)
m, var, skw, kur = spt.norm.stats(loc=5,scale=2,moments='mvsk')
print(m,var,skw,kur)
x = np.linspace(spt.norm.ppf(0.01,loc=5,scale=2),spt.norm.ppf(0.99,loc=5,scale=2), 1000)
ax.plot(x, spt.norm.pdf(x,loc=5,scale=2),'r-', lw=5, alpha=0.6, label='normal pdf')
rv = spt.norm.rvs(loc=5,scale=2,size=3000)
ax.hist(rv, density=True, histtype='stepfilled', alpha=0.2)
plt.show()
2. 카이제곱분포

카이제곱분포의 가법성

자유도
제곱합에 포함되는 ‘독립적인 항’의 개수
표본분산의 자유도는?

실습코드
# Chi-squared distribution
fig, ax = plt.subplots(1, 1)
df = 5
m, var, skw, kur = spt.chi2.stats(df, moments='mvsk')
print(m,var,skw,kur)
x = np.linspace(spt.chi2.ppf(0.01, df),spt.chi2.ppf(0.99, df), 1000)
ax.plot(x, spt.chi2.pdf(x, df),'r-', lw=5, alpha=0.6, label='chi-squared pdf')
rv = spt.chi2.rvs(df, size=10000)
ax.hist(rv, density=True, histtype='stepfilled', alpha=0.2)
plt.show()
3. T 분포
- 표준정규분포를 따르는 확률변수를 Z라 하고, Z와는 독립적으로 자유도 ν인 카이제곱 분포를 따르는 확률변수를 Y라한다.
- 모집단이 1개 또는 2개일때 많이 사용
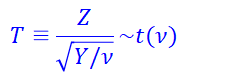
실습코드
# student's t distribution
fig, ax = plt.subplots(1, 1)
df = 3
m, var, skw, kur = spt.t.stats(df, moments='mvsk')
print(m,var,skw,kur)
x = np.linspace(spt.t.ppf(0.01, df),spt.t.ppf(0.99, df), 100)
ax.plot(x, spt.t.pdf(x, df),'r-', lw=5, alpha=0.6, label='student''s t pdf')
rv = spt.t.rvs(df, size=3000)
ax.hist(rv, density=True, histtype='stepfilled', alpha=0.2)
plt.show()
3. F 분포
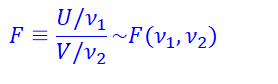
실습코드
# F distribution
fig, ax = plt.subplots(1, 1)
dfn, dfd = 29, 18
m, var, skw, kur = spt.f.stats(dfn, dfd, moments='mvsk')
print(m,var,skw,kur)
x = np.linspace(spt.f.ppf(0.01, dfn, dfd),spt.f.ppf(0.99, dfn, dfd), 100)
ax.plot(x, spt.f.pdf(x, dfn, dfd),'r-', lw=5, alpha=0.6, label='F pdf')
rv = spt.f.rvs(dfn, dfd, size=2000)
ax.hist(rv, density=True, histtype='stepfilled', alpha=0.2)
plt.show()
320x100
320x100
'빅데이터 관련 자료 > 수학&x통계' 카테고리의 다른 글
| 파이썬 데이터 분석을 위한 수학 & 통계 - 3회차 - 3 (0) | 2021.08.17 |
|---|---|
| 파이썬 데이터 분석을 위한 수학 & 통계 - 3회차 - 2 (0) | 2021.08.17 |
| 파이썬 데이터 분석을 위한 수학 & 통계 - 2회차 - 2 (0) | 2021.08.11 |
| 파이썬 데이터 분석을 위한 수학 & 통계 - 2회차 - 1 (0) | 2021.08.11 |
| 파이썬 데이터 분석을 위한 수학 & 통계 - 1회차 (0) | 2021.08.09 |